Problem

Find the number of 3 digit natural numbers that are divisible by 2 or 3 but not by 7.

Solution

Let the set U be set of the 3 digit numbers (i.e. numbers from 100 to 999, both numbers inclusive). Let the sets \(D_2\), \(D_3\) and \(D_7\) be subsets of U such that they are the sets of numbers divisible by 2, 3 and 7 respectively. Similarly, the let sets \(D_{23}\), \(D_{37}\), \(D_{27}\) and \(D_{237}\) denote numbers divisible by 2 and 3, 3 and 7; 2 and 7; 2, 3 and 7 respectively.

The count of numbers that are divisible by 2 or 3 but not by 7 is equal to \( | D_2 \cup D_3 \cup D_7 | - | D_7| \) (see diagram below).

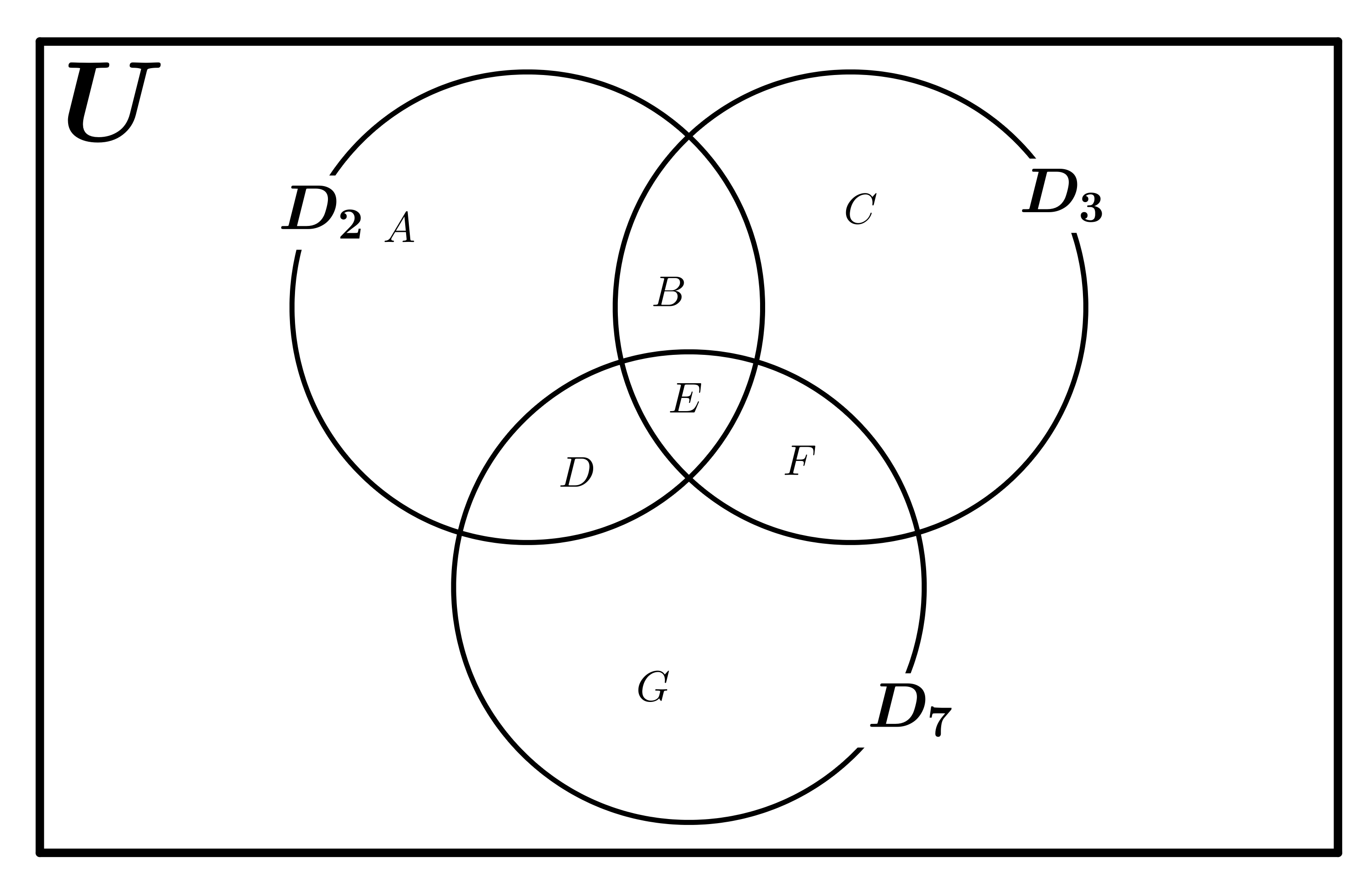
By the principle of inclusion and exclusion: \( |D_2 \cup D_3 \cup D_7 | =\)\( |D_2| + |D_3| + |D_7| - |D_2 \cap D_3| \)\(- |D_2 \cap D_7| \)\(- |D_3 \cap D_7|\)\( + |D_2 \cap D_3 \cap D_7 |\)

Hence, \(A + B + C =\)\( |D_2| + |D_3|\)\( - |D_2 \cap D_3| - |D_2 \cap D_7|\)\( - |D_3 \cap D_7|\)\( + |D_2 \cap D_3 \cap D_7 | \).

The numbers in U that are divisible by 2 are: 100, 102, 104 … 998. This is an A.P. that starts from 100 with difference of 2 between successive terms. Hence, \(100 + 2(|D_2| - 1) = 998\). Therefore, \(|D_2| = 450\). Or alternatively, the numbers between 100 and 999 that are divisible by 2 are \( \lfloor\frac{999}{2}\rfloor - \lfloor \frac{99}{2} \rfloor = 450 \).

The numbers in U that are divisible by 3 are: 102, 105, 108 … 999. This is an A.P. that starts from 102 with difference of 3 between successive terms. Hence, \(102 + 3(|D_3| - 1) = 999\). Therefore, \(|D_3| = 300\).

The numbers in U that are divisible by 2 and 3 (i.e \(2\times 3=6\)) are: 102, 108, 114 … 996. This is an A.P. that starts from 102 with difference of 6 between successive terms. Hence, \(102 + 6(|D_{23}| - 1) = 996\). Therefore, \(|D_{23}| = 150\).

The numbers in U that are divisible by 2 and 7 (i.e \(2 \times 7 = 14\)) are: 112, 126, … 994. This is an A.P. that starts from 112 with difference of 14 between successive terms. Hence, \(112 + 14(|D_{27}| - 1) = 966\). Therefore, \(|D_{27}| = 64\).

The numbers in U that are divisible by 3 and 7 (i.e \(3\times 7=21\)) are: 105, 126, … 987. This is an A.P. that starts from 105 with difference of 21 between successive terms. Hence, \(105 + 21(|D_{37}| - 1) = 987\). Therefore, \(|D_{37}| = 43\).

The numbers in U that are divisible by 2, 3 and 7 (i.e \(2 \times 3 \times 7 = 42\)) are: 126, (126 + 42) … 966. This is an A.P. that starts from 126 with difference of 42 between successive terms. Hence, \(126 + 41(|D_{237}| - 1) = 966\). Therefore, \(D_{237} = 21\).

Substituting the values : \(A + B + C = |D_2| + |D_3| - |D_{23}| - |D_{27}| - |D_{37}| + |D_{237}|\) we get \( A + B + C = 450 + 300 - 150 - 64 - 43 + 21 = 514\). Thus, the answer is 514.